A new source of gravitation waves: particle production from bubble collision

Here I introduce a new paper that appeared on arXiv at the end of last year, from the particle physics and cosmology group in JHU, Tokyo U and DESY.

While the title is pretty clear about its content, some keywords might be difficult for people outside this specific topic.

The most important one is: first-order phase transition.

Phase transition is a pretty widely-applied word. Things familiar to us, such as gas-liquid transition, solid-liquid transition, are all first-order phase transitions. The character is the existence of the specific boundary between these phases. On the contrary, if no such a boundary exists between phases, we call it second-order phase transition. Example could be difficult to find in daily life for second-order phase transition. The most popular example may be the ferromagnetic phase transition that we learned in our undergrad.

Phase transitions also happen in the early universe. For example, we know that particles acquire there masses from their interactions with Higgs. But at the very early time of the universe, these masses do not exist. Higgs, as well as other particles, is massless. When the universe gradually cools down, masses are generated below a certain critical temperature. This process is also a phase transition, known as the electroweak phase transition (EWPT).

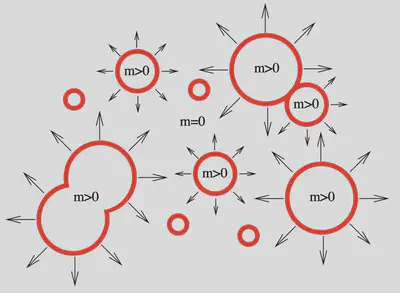
There is no clear evidence for now whether EWPT is first-order or not. While the Standard Model (SM) predicts a second-order PT, beyond SM physics may modify it to be first-order. Even though EWPT finally turns out to be second-order, there is highly a chance in the early universe that a similar phase transition existing much earlier than EWPT that can be first-order.

If the EWPT is first-order, scenario in the above picture can happen. Particle masses shift from 0 to a finite number, and there is a boundary between these two. The region inside the boundary is known as the bubble.

This bubble really behaves like a physical wall. It can collide with particles surrounding it, and it can collide with another bubble wall. And indeed, as the phase transition proceed, the bubble walls expand and really collide with each other.

Just as the collision between two balls in the real world can create sound wave, the bubble collisions can create gravitational waves (GW).

There has been answers about how the GWs are created. In one word, it comes from the breaking of the spherical symmetry of the stress-energy tensor in the universe. If the universe is made of homogenous things, the stress-energy tensor is apparently homogenous and spherical symmetry is kept. However, various perturbations can break this symmetry. Einstein’s equation tells us that GW can be produced once the stress-energy tensor is no longer spherically symmetric.

If we talk about these things in the context of bubbles, there are three known-types of GW sources.

The first one is the bubble collision itself.

The bubble is nothing but a shell of masses. It carries energy. If the bubble is not re-shaping, not colliding, but just expanding, the stress-energy tensor is still spherically symmetric, and no GW is produce.

However, when the bubbles collide with each other, the shape of shell changes. e.g. In the above figure, bubble merges, and the shells disappear in the region where bubbles overlap. This is not spherically symmetric, and GW can be produced.

See: Gravitational waves from bubble collisions: analytic derivation

The second one is the sound wave after the bubble collision.

The early universe is not a vacuum, but rather filled by plasma. The plasma is the most perfect fluid. Sound wave can of course be produced by these bubbles.

Again, if the bubbles are just expanding, the sound waves are spherically symmetric, and no GW can be produced. The key is that the spherical symmetry in the sound wave is also broken by the bubble collision. GW are thus source by this sound wave.

See：Sound shell model for acoustic gravitational wave production at a first-order phase transition in the early Universe

The third part is MHD turbulence. I know very rare things about it, and I’ll not review it here.

These three sources has been known as all the sources of GW during bubble collision in the past decades. However, the paper introduced today provides a new possible source: bubble collision can produce particles, whose energy distribution is also non-spherically-symmetric, and thus GW can be sourced.

There has been known papers talking about particle production by bubbles. Fast-moving bubbles are similar to colliders. Heavy particles can be created. The more energy the bubble shell carries, the heavier particle it can create. This particle production mechanism could be found in a paper earlier last year. Nonthermal Heavy Dark Matter from a First-Order Phase Transition

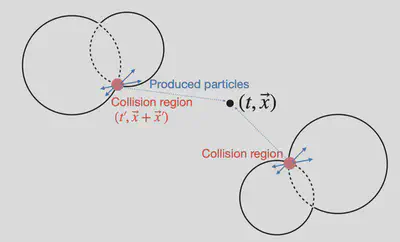
Apparently, since spherical symmetry is already broken by the collision, the distribution of the energy carries by the particles has definitely no spherical symmetry. GW is thus sourced.

The next question is: is the bubble energy large enough to create this enough particles?

For this question, this paper gives an answer based on the widely-believed knowledge: the wall only carries non-negligible fraction of released energy during phase transition only in vacuum or in a near-vacuum environment. In the presence of plasma, most released energy are taken by the plasma. This is similar to the condition under which bubble collision contribution to GW is non-negligible.

The discussion of GW produced by the bubble is thus categorized in to two: Vacuum/near vacuum, or in dense plasma. The first one typically appears in supercooling phase transitions, or in some quantum tunneling case under low temperature. The latter one is irrelevant for this article.

Under the first condition, this new source can modify the GW signal as shown in the following plot.

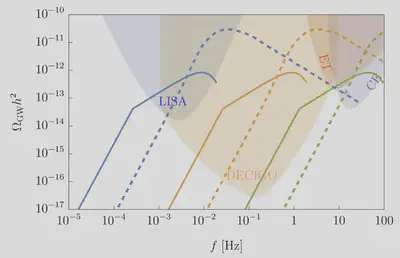
The dashed lines are the original ones from bubble collision. The solid lines are from the new source. The total should be the sum of those. We can see that the GW signal in the low-frequency region is significantly enhanced.

I haven’t checked the calculation in detail, but it seems good to me now. This article should have a profound impact. From now, papers talking about vacuum phase transitions should all utilize this result.