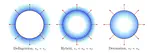
Electroweak (-like) baryogenesis
 Figure created by J. Cline, hep-ph/0609145
Figure created by J. Cline, hep-ph/0609145
Introduction
It is known that Higgs potential is spontaneously broken in the current universe. However, if no new physics is appearing, the symmetry would be restored at high temperature. The transition from the restored Higgs potential symmetric phase to the broken phase during the universe cooling down is called the electroweak phase transition (EWPT).
If new physics appear, depending on the form of new physics, the phase transition may be enhanced, or on the other hand, the symmetry may not be restored at high temperature. Both are strongly motivated for various problems, especially by the baryogenesis problem. Specifically, in 1985, it was presented that electroweak phase transition may provide the necessary condition for baryogenesis if it’s strongly first order. This mechanism is known as electroweak baryogenesis (EWBG). However, the phase transition is known to be a smooth crossover after Higgs mass was measured.
This is not the end of the story. People know that a simple scalar extension in the Higgs sector could enhance the phase transition so that a strongly first-order phase transition may appear. On the other hand, if the real model of this world contains a larger gauge group and multiple electroweak-like phase transitions in the early history, this mechanism may still work at some moment.
At least, there are a few things below that worth investigating.
Models including electroweak-like phase transition at high energy scale
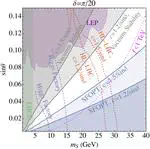
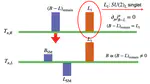
We have tons of models that include a gauge group symmetry breaking pattern at high energy scale. For example, the parity-symmetric model contains a phase transition $SU(2)_R \times U(1)_X \to U(1)_Y$. More interesting phase transition also appears, for example, in GUT theroy, in twin-Higgs theory, and so forth. The phase transition happens for different scalar fields, or have different interactions, or have different coupling strength, compared to the standard model.
For example, in parity-symmetric model, the running coupling, especially the running of $\lambda$, will make the achievement of a strong first-order phase transition much easier.
It could be a very interesting direction to investigate the phase transition and phase thermal history of those models.
Computation of phase transition quantities
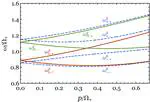
On the other hand, the electroweak phase transition is very technical. The prediction of baryon asymmetry is pretty controversial. These include (but not limited to):
- Wall velocity
- Baryon number asymmetry
- Phase transition strength
Without a trustable method, we cannot make prediction for models. Given the strong motivation for electroweak (-like) phase transition stated before, it could be very valuable to improve the computation of various quantities in the phase transition.